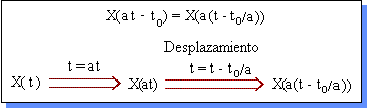
Escalamiento en Tiempo |
x2(t) = x1(at) |
x2[n] = x1[an] |
| Se consigue mediante un escalamiento lineal de la variable independiente. | ||
| Gráficamente equivale a ensanchar (a < 1) o encoger (a > 1) la señal. | ||
| Si se trata de una señal discreta, esta operación originará la aparición de nuevas muestras iguales a cero (a < 1) o la desaparición de algunas muestras (a > 1), debido a que la variable independiente "n" solo puede tomar valores enteros. | ||
| Un ejemplo práctico de la operación (escalamiento en tiempo) sería: | ||
| Si x(t) es una señal de audio en una grabadora de cinta, x( 2 t ) sería la misma grabación pero reproducida al doble de la velocidad) y x( ½ t ) reproducida a la mitad de la velocidad. | ||
| Cuando se tiene la operación de escalamiento en tiempo acompañada de un desplazamiento, primero se debe escalar la señal y luego se debe desplazar. Estas operaciones tampoco son conmutativas entre sí. | ||
| Cuando se desee escalar en tiempo y desplazar una señal, se debe proceder de la siguiente manera. | ||
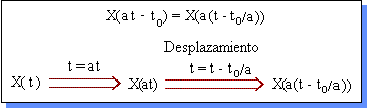 |
||
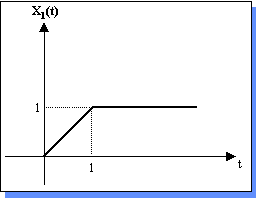
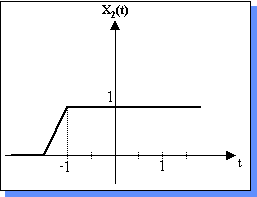
| Ejemplo: x2(t) = x1(2t + 3) | ||
 |
 |
|
| Ejemplo: x2[n] = x1[ ½ n + 1] | ||
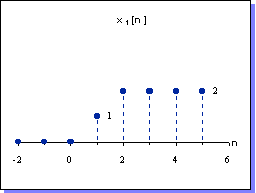 |
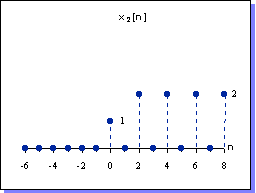 |
|
![]()
![]()