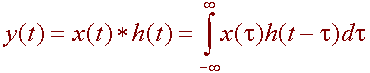
Convolución de Señales |
|
 |
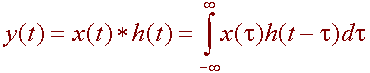Esta operación es muy usada en comunicaciones, análisis armónico, etc., permitiendo encontrar fácilmente muchos resultados importantes. | |
|
La
integral del lado derecho, es decir la integral de convolución, la, podemos interpretar
como el área bajo la curva resultante del producto entre x(  ) y h(
t - ). |
|
|
Para esta integral, se han realizado los siguientes cambios de variable: | |
 |
Para x( t ) se
hace el cambio de variable independiente, t =  . |
|
|
Para h( t ) se
hace el cambio de variable independiente, t = , además se refleja y
se desplaza la señal t unidades. |
|
|
El cálculo de la integral se puede realizar de dos maneras, analíticamente (resolviendo las integrales planteadas) o gráficamente (calculando las áreas respectivas a partir de los gráficos realizados para las señales). | |
|
La
convolución con  (t) se calcula valiéndose de la propiedad de
separación de la función (t), que permite escribir la función
x(t) como la suma de infinitos pulso pesados: |
|
 |
||
|
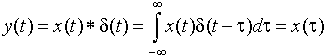Además se puede verificar que: | |
|
f ( t ) ¤  ( t - T ) = f ( t - T ). |
|
|
f ( t - T1
) ¤ ( t - T2 ) = f ( t - T1 - T2
). |
|
|
( t - T1 ) ¤ ( t - T2 )
= ( t - T1 - T2 ). |
|
|
f ( t ) ¤ [( t + T ) + ( t - T ) = f ( t + T ) + f ( t - T
). |
|
|
Ejemplo de cálculo: | |||
| Primero se grafican las señales x ( t ) y h ( t ) : |  |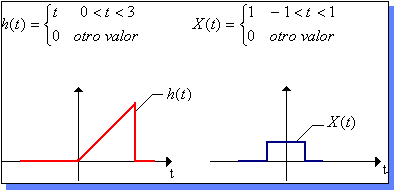
|||
| Se
cambia la variable t por y se refleja h ( t ) :
|
||||
 |
||||
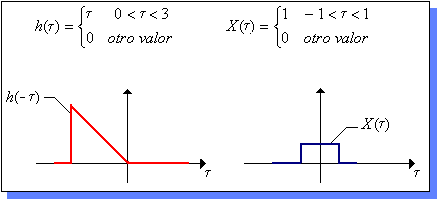| Ahora
se desplaza h ( - ), t unidades, consiguiendo
h ( t - ) , o lo que es lo mismo
h ( - ( - t ) ) : |
||||
 |
||||
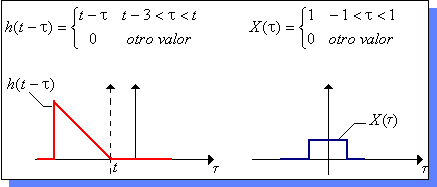| Luego
se deben tomar en cuenta los diferentes intervalos de t para los cuales cambia la
expresión de x ( t ) · h ( t - ), resolviendo la integral de convolución para cada intervalo. |
||||
El primer
intervalo a considerar sería -  < t < -1,
en el cual se tiene, para cualquier valor de t: |
 |
|||
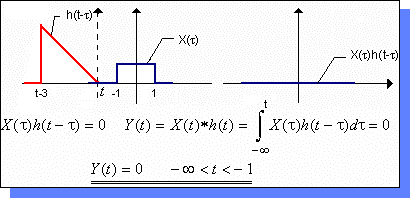| El segundo intervalo a considerar sería - 1 < t < 1, en el cual se tiene, para cualquier valor de t: | ||||
 |
||||
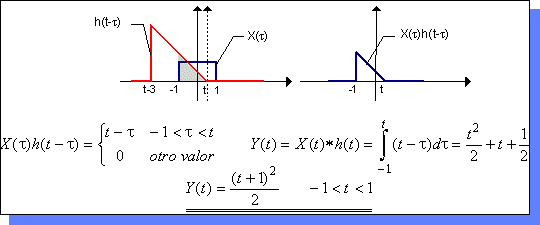| El siguiente intervalo a considerar sería 1 < t < 2, en donde: | ||||
 |
||||
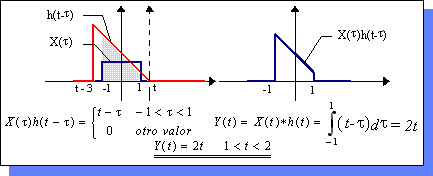| El cuarto intervalo a considerar sería 2 < t < 4, en el cual, para cualquier valor de t: | ||||
 |
||||
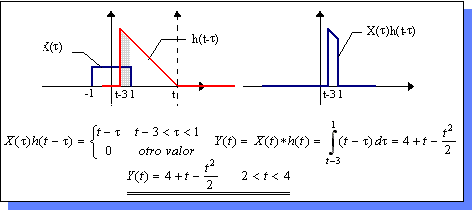| El último
intervalo a considerar sería 4< t < , en el cual se obtiene para cualquier valor de t: |
 |
|||
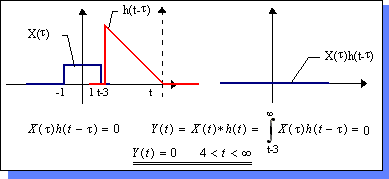| Finalmente, resumiendo el resultado de x ( t ) ¤ h ( t ) en un gráfico, se obtiene: | ||||
 |
||||
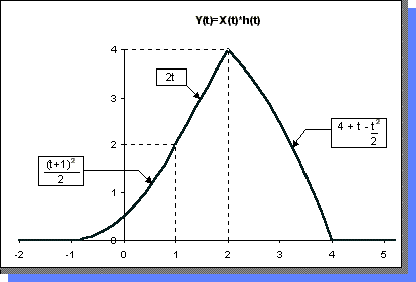