
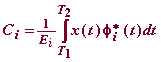
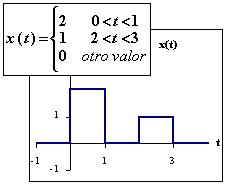
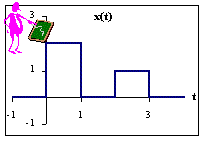
Señal x(t) de duración finita (energía finita), representada en términos de Componentes Ortonormales en el intervalo (0,3):
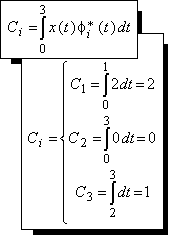
x ( t ) = 2ø1
( t ) + 0ø2 ( t ) + ø3 ( t )
Componente Ortonormales:
Componentes Ortogonales y Ortonormales de una Señal Arbitraria |
| Las señales ortonormales facilitan la representación de señales arbitrarias en términos de una suma infinita de componentes. | ||
| Si øi (t) es un Conjunto de Señales Ortonormales en un intervalo ( T1 ,T2 ) y x(t) es una señal arbitraria con energía finita en ( T1 ,T2 ), podemos escribir: | ||
|
||
| Si øi (t) es un Conjunto de Señales Ortogonales los coeficientes Ci serán: | 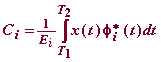 |
|
| Estas expresiones se conocen como la "Forma Generalizada de la Serie de Fourier" y los Ci serían los "Coeficientes de Fourier". | ||
Ejemplo:
|
|
|
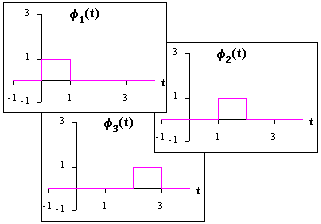
| Conjunto de Señales Ortonormales: | ||
 |
||
|
||
Componente Ortonormales: |
||
x ( t ) = 2ø1 ( t ) + ø3 ( t ) »»  |
||
![]()
![]()